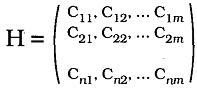Комбинированный прогноз

некоторая обобщающая оценка, получаемая на основе формального или неформального объединения частных прогнозов, чаще всего путем суммирования их с определенными весовыми коэффициентами. В практике прогнозирования нередки случаи, когда прогноз одного и того же показателя получают различными методами, дающими спектр не всегда совпадающих результатов. В некоторых случаях, напр., для оценки интервала изменения прогнозируемого показателя, этого вполне достаточно. Если же требуется получить не интервальный, а точечный прогноз, приходится решать проблему выбора наиболее достоверного прогноза, либо использовать все полученные прогнозные оценки для расчета так называемого комбинированного (сводного) прогноза. Необходимое условие его использования — наличие спектра прогнозных оценок одного и того же показателя, полученных в различных моделях или процедурах. Для получения прогноза осуществляется подбор наиболее адекватной модели описания данных, характеризующих динамику прогнозируемого показателя за предшествующие годы. Исследователь, как правило, располагает некоторым набором взаимно дополняющих моделей прогнозирования одного и того же показателя. Задача комбинирования прогнозов сводится к нахождению такого набора весов, который обеспечивает минимальную ошибку комбинированного прогноза. Рассмотрим общую схему построения комбинированного прогноза анализируемого показателя. Предполагается, что имеется m прогностических моделей одного и того же показателя Y. Эти модели, по предположению, могут отличаться друг от друга тем, что с разной степенью адекватности описывают различные стороны моделируемого показателя (явления). В модель могут включаться различные факторы (аргументы модели), влияющие на формирование моделируемого показателя; сами модели могут иметь различный вид (линейный, нелинейный), параметры моделей также могут быть различными. В этом случае возникает так называемый «спектр прогнозных оценок», что открывает принципиальную возможность построения комбинированного прогноза, который по своим свойствам должен превосходить (или, как минимум, не ухудшать лучший из исходных прогнозов. Предполагается также, что объем и свойства имеющихся данных позволяют рассматривать комбинирование частных прогнозов как формальную математическую задачу, напр., применять регрессионные методы, а сами данные представлять непрерывными динамическими рядами. Комбинирование прогнозов проводится с целью повышения качества прогнозирования, универсальным критерием которого обычно выступает точность прогнозирования, измеряемая абсолютной либо относительной ошибками прогнозирования. Строго говоря, точность прогнозирования не является единственным критерием качества прогнозов, возможны и другие критерии качества, например, надежность, чувствительность к изменениям и другое, с целью достижения которых может строиться комбинированный прогноз. Поэтому цель комбинирования прогнозов — уменьшение величины ошибки прогнозирования (точнее, ее некоторой функции). Комбинирование частных прогнозов может быть, вообще говоря, как линейным, так и нелинейным. Рассмотрим линейные модели комбинирования частных прогнозов с постоянными коэффициентами. Пусть имеется m моделей некоторого показателя (результирующей переменной). По этим моделям в интервале получены прогнозы. Следует найти такой комбинированный прогноз: (1) чтобы абсолютная ошибка прогнозирования , или относительная ошибка прогнозирования была достаточно мала. В (1) параметры {Ci} носят название коэффициентов комбинирования. Когда речь идет об экономических показателях, имеющих только положительные значения (и не обращающихся в нуль), использование относительных ошибок прогнозирования предпочтительнее, так как дает возможность абстрагироваться от абсолютных величин результирующего показателя. В этом случае выражение для относительной ошибки комбинировпнного прогноза принимает вид: 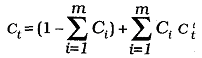где C it — относительныеошибки прогнозирования по i-ой модели ( i = 1,m). Чтобы ошибка комбинированного прогноза не содержала систематическую составляющую, сумма коэффициентов комбинирования должна быть равна единице: 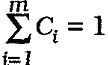. Отсюда: 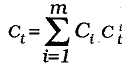(2). Обычно исходят из того, что коэффициенты комбинирования {Ci} представляют собой меру доверия к частным прогнозам и колеблются от 0 (в этом случае частный прогноз не включается в комбинированный прогноз) до 1 (в этом случае все остальные прогнозы не включаются в комбинированный прогноз.). Таким образом, на коэффициенты комбинирования накладываются ограничения вида равенств и неравенств одновременно: 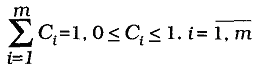(3).

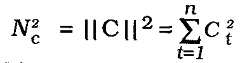Обычно в качестве меры точности прогнозов используется норма вектора относительных ошибок: на интервале прогнозирования t = 1,n. При вероятностной интерпретации ошибок в качестве меры точности используют аналогичную величину — дисперсию ошибок. Таким образом, при построении комбинированного прогноза по частным прогнозам исследователи располагают исходными данными в виде матрицы H ретроспективных относительных ошибок прогнозирования:

 где c_ij — относительная ошибка прогноза (или аппроксимации) по j-ой модели в i-й момент времени (в i-й точке). Размерность матрицы H равна (nxm).

По данным матрицы H необходимо найти коэффициенты (веса) комбинирования {Ci ; i = 1,n }, удовлетворяющие условиям (3). Эти коэффициенты находят из условия минимизации нормы или дисперсии вектора ошибок комбинированного прогноза с ограничениями типа уравнений и неравенств одновременно:

вернуться к списку